本ページでは以下のページを要約するとともに、個人的な解説も記載しています。独特な解釈をしている部分があるので、誤りなどの指摘はtwitterまでお願いします。
参考ページ
Supervised learning: predicting an output variable from high-dimensional observations — scikit-learn 1.1.2 documentation
https://scikit-learn.org/stable/tutorial/statistical_inference/supervised_learning.html
閲覧日:2022年10月12日
教師あり学習とは
教師あり学習は観測された学習用のデータXと、「ターゲット」や「ラベル」とよばれる、学習データに紐づく予測しようとしているデータyの2つのデータをセットで学習します。
ほとんどの場合、ラベルは1次元配列になります。
教師あり学習で使用するestimatorは、モデルを学習させるためのメソッドfit(X,y)と、学習データXを与えたときに予測されたラベルyを返すメソッドpredict(X)を持ちます。
scikit-learn で分類を行う場合、ラベルyは整数または文字列の配列です。
最近傍と次元の呪い
アヤメの分類:
アヤメのデータセットは、花弁とがく片の長さと幅から 3 種類のアヤメ (Setosa、Versicolour、Virginica) に分類するタスクです。
以下のコードでデータの詳細を確認できます。
アヤメの種類を0,1,2の数値で表しています。
import numpy as np
from sklearn import datasets
iris_X, iris_y = datasets.load_iris(return_X_y=True)
np.unique(iris_y)
#array([0, 1, 2])
※PCAで3次元に学習データを変換させたのち、データを可視化すると以下のようになります。オリジナルコードなので汚くてすみません。
from sklearn.decomposition import PCA
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
#主成分分析の実行
pca = PCA()
pca.fit(iris_X)
score = pd.DataFrame(pca.transform(iris_X))
x = score[0]
y = score[1]
z = score[2]
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
for i in range(iris_y.size):
if iris_y[i] == 0:
ax.scatter(x[i], y[i], z[i], color='red')
elif iris_y[i] == 1:
ax.scatter(x[i], y[i], z[i], color='orange')
else:
ax.scatter(x[i], y[i], z[i], color='gray')
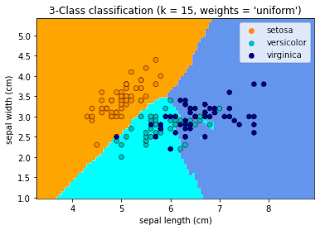
k最近傍法
最も単純なアルゴリズムがk最近傍法です。未知のデータを与えた場合、学習に使ったデータと比較して特徴が近いデータと同じ予測値を出力します。
詳細はこちら。今後ブログにもしていく予定です。
トレーニングセットとテストセット
AIモデルを作成する際は、未知のデータでの性能を考慮しません。しかし、学習データを使ってAIモデルを作成するという性質上、学習データを使って予測した結果を評価すると不当に高い性能となってしまいます。正当な評価をするためには未知のデータが必要です。しかし、未知のデータとセットで正しい予測結果のデータも必要となると、タスクによってはデータの収集が難しいことがあります。そのようなことから、既存のデータをトレーニングデータとテストデータで分割することが多くなっています。
KNN (k 最近傍法) での分類の例
※出し方はこちら# アヤメのデータをトレーニングデータとテストデータに分割
# 分割する前に配列をランダムに並べ替えています。
np.random.seed(0)
indices = np.random.permutation(len(iris_X))
#後ろの10個のデータをテストデータとして使用
iris_X_train = iris_X[indices[:-10]]
iris_y_train = iris_y[indices[:-10]]
iris_X_test = iris_X[indices[-10:]]
iris_y_test = iris_y[indices[-10:]]
# Create and fit a nearest-neighbor classifier
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier()
knn.fit(iris_X_train, iris_y_train)
#KNeighborsClassifier()
knn.predict(iris_X_test)
#array([1, 2, 1, 0, 0, 0, 2, 1, 2, 0])
iris_y_test
#array([1, 1, 1, 0, 0, 0, 2, 1, 2, 0])
次元の呪い
k近傍法に限らず、特長量が増えると計算量がグッと増えます。例えばk近傍法であれば、近くのデータとの距離を計算しています。2次元の特長量であれば大したことありませんが、これが10次元100次元となると計算量が指数関数的に増加してしまいます。そのような問題のことを次元の呪いと呼びます。